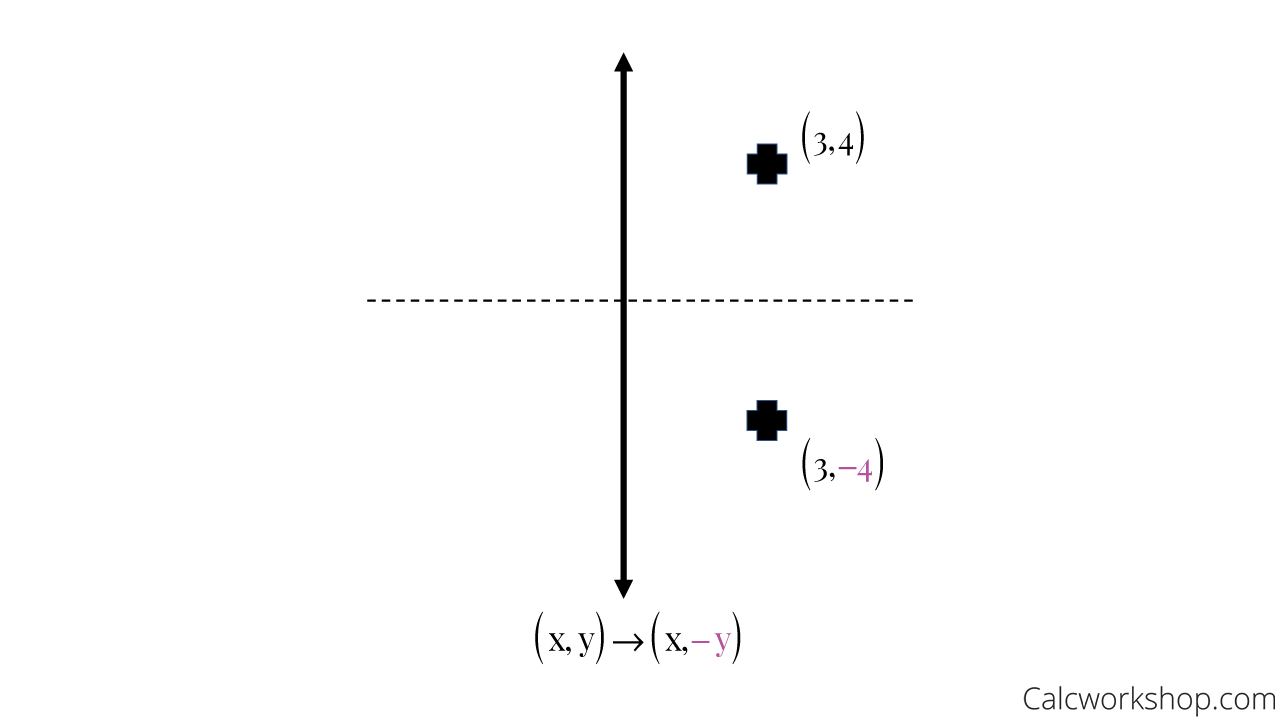
Select three options b d e wrong ΔA'B'C' was constructed using ΔABC and line segment EH For to be the line of reflection between and , which statements must be true?What is the rule for the following reflection?To write a rule for this reflection you would write rx−axis(x,y) → (x,−y) Notation Rule A notation rule has the following form ry−axisA → B = ry−axis(x,y) → (−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been multiplied by 1
Determining Reflections Video Khan Academy
How to reflect over y=x+1
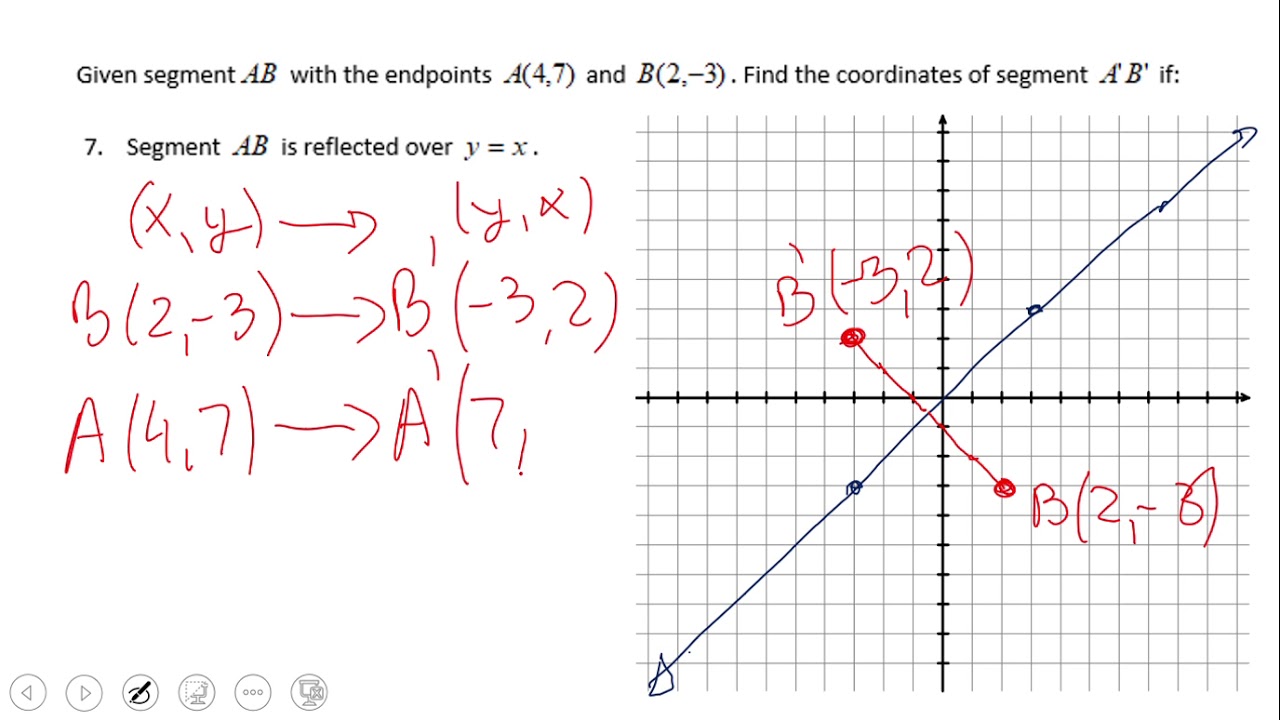
How to reflect over y=x+1-The rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shownX y J Z L 2) translation 4 units right and 1 unit down x y Y F G 3) translation 1 unit right and 1 unit up x y E J T M 4) reflection across the xaxis x y M C J K Write a rule to describe each transformation 5) x y H C B H' C' B' 6) x y P D E I D' E' I' P'1




How To Find A Reflection Image
To write a rule for this reflection you would write rx−axis(x,y) → (x,−y) Notation Rule A notation rule has the following form ry−axisA → B = ry−axis(x,y) → (−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been multiplied by 1To write a rule for this reflection you would write rx−axis(x,y) → (x,−y) Notation Rule A notation rule has the following form ry−axisA → B = ry−axis(x,y) → (−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been multiplied by 1 What are the two rules of reflection?A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection Let's look at two very common reflections a horizontal reflection and a vertical reflection
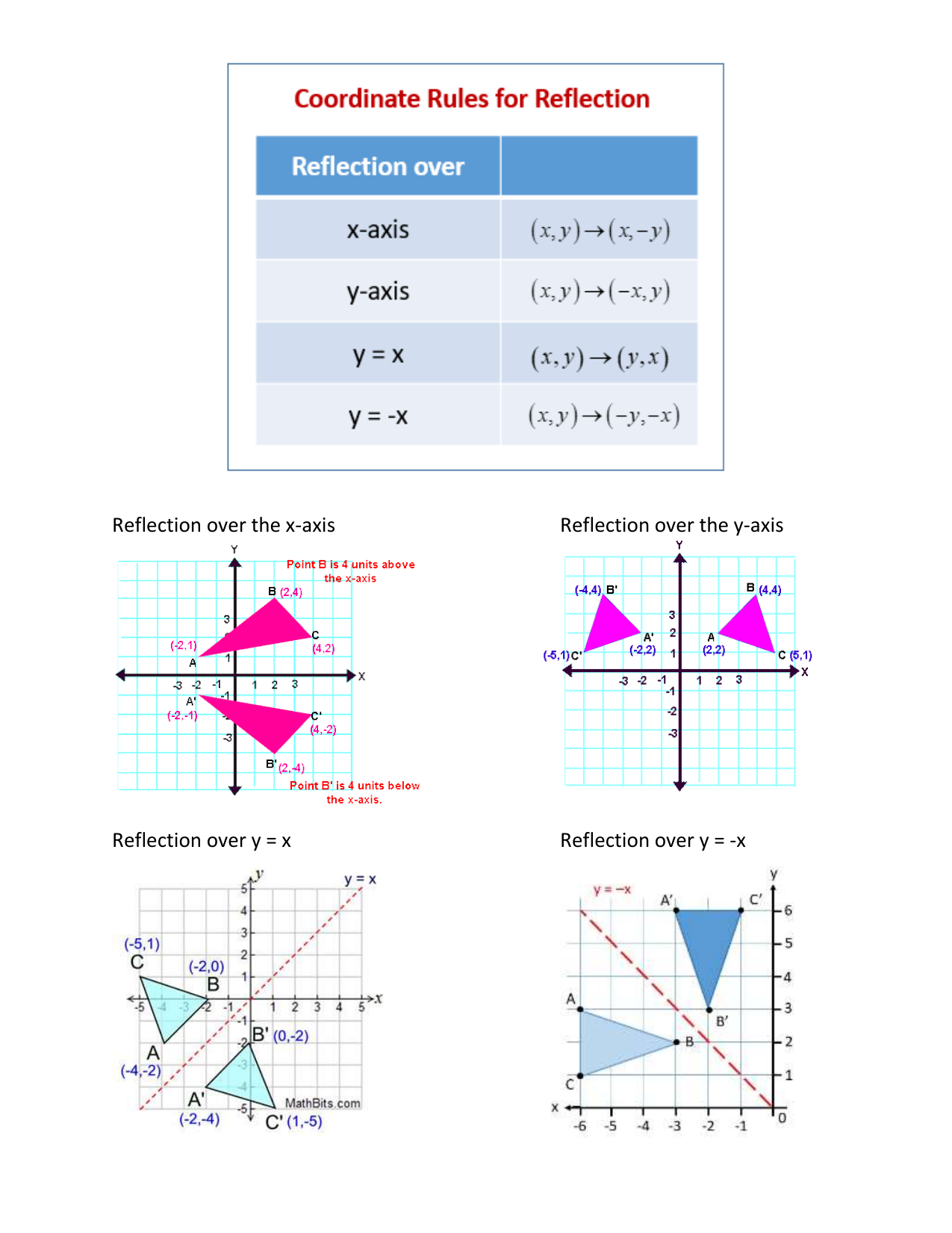
3 What is the rule for reflection? Answer A reflection is an example of a transformation that takes a shape (called the preimage) and flips it across a line (called the line of reflection) to create a new shape (called the image) The most common lines of reflection are the xaxis, the yaxis, or the lines y=x or y=−x The xaxis, Reflection across the xaxis (3,2)→(3,−2) ie for reflection across the xaxis the xNotation Rule A notation rule has the following form ry−axisA → B = ry−axis(x,y) → (−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been multiplied by 1
Reflection across the xaxis composition translation of negative 6 units x, 1 unit y translation of negative 6 units x, 1 unit y composition reflection across the xaxis 90 degree rotation about point 0 composition translation of Answers 2 on a question Which rule describes the composition of transformations that maps preimage abcd to final image abcd?Rxaxis (x, y) → (x, y) ryaxis (x, y) → (x, y) c Which statements must be true about the reflection of ΔXYZ across ?



1




Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaReflect over x= 1;👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x




Geometry Identify The Reflection Rule On A Coordinate Plane That Verifies That Triangle A 1 7 Brainly Com




Identify The Glide Reflection Rule In The Given Figure Question 8 Options Translation X Y X Brainly Com
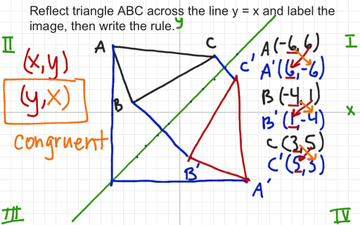
When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection over the line y=x By following the notation, we would swap the xvalue and the yvalueC figure C and R(1, 2) It is translated according to the rule (x, y) → (x 2, y 16) What is the yvalue of P'?Is over of equals percent over 100



Reflection An Isometry Or Rigid Motion In Which A Figure Is Flipped Giving Its Image An Opposite Orientation Ppt Download




Reflection Over The Y X Line Youtube
To write a rule for this reflection you would write rx−axis (x,y) → (x,−y) Notation Rule A notation rule has the following form ry−axisA → B = ry−axis (x,y) → (−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been multiplied by 1 What is the formula of reflection?Describe each transformation using an algebraic rule 1 Reflection across y=x 2 90o rotation clockwise 3 Reflection across the yaxis followed by a translation up 4, left 5 Complete the matrix multiplication problem below2 5 3 6 0 14 7 8 09 1 = Complete each matrix multiplication and describe the translationAnswer choices Reflection across y = −1 Reflection across y = 1 Reflection across x = −1 Reflection across y = −x answer explanation s Topics Question 15 SURVEY Ungraded 60 seconds Report an issue




Reflection Mathbitsnotebook A1 Ccss Math




Algebraic Representations Of Reflections
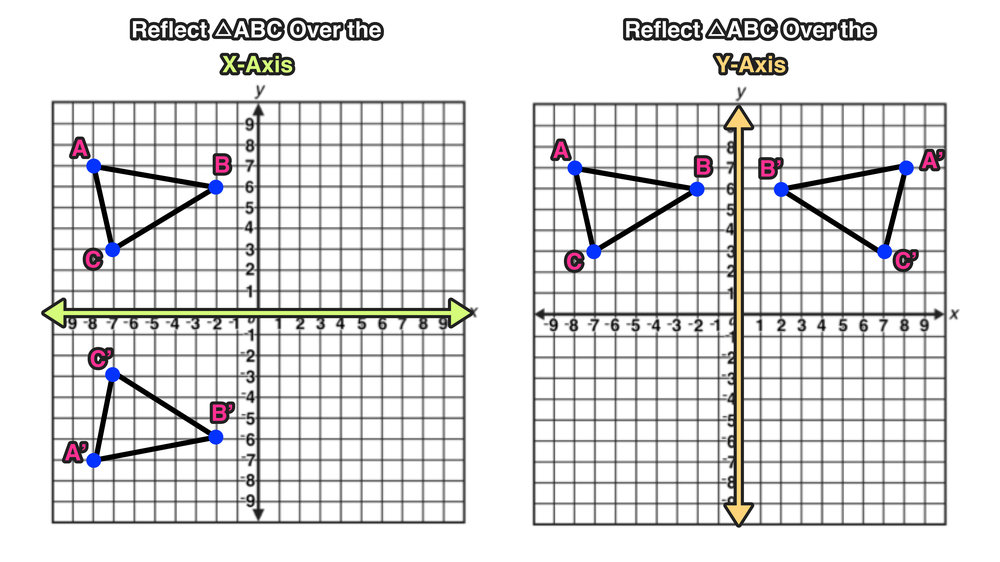
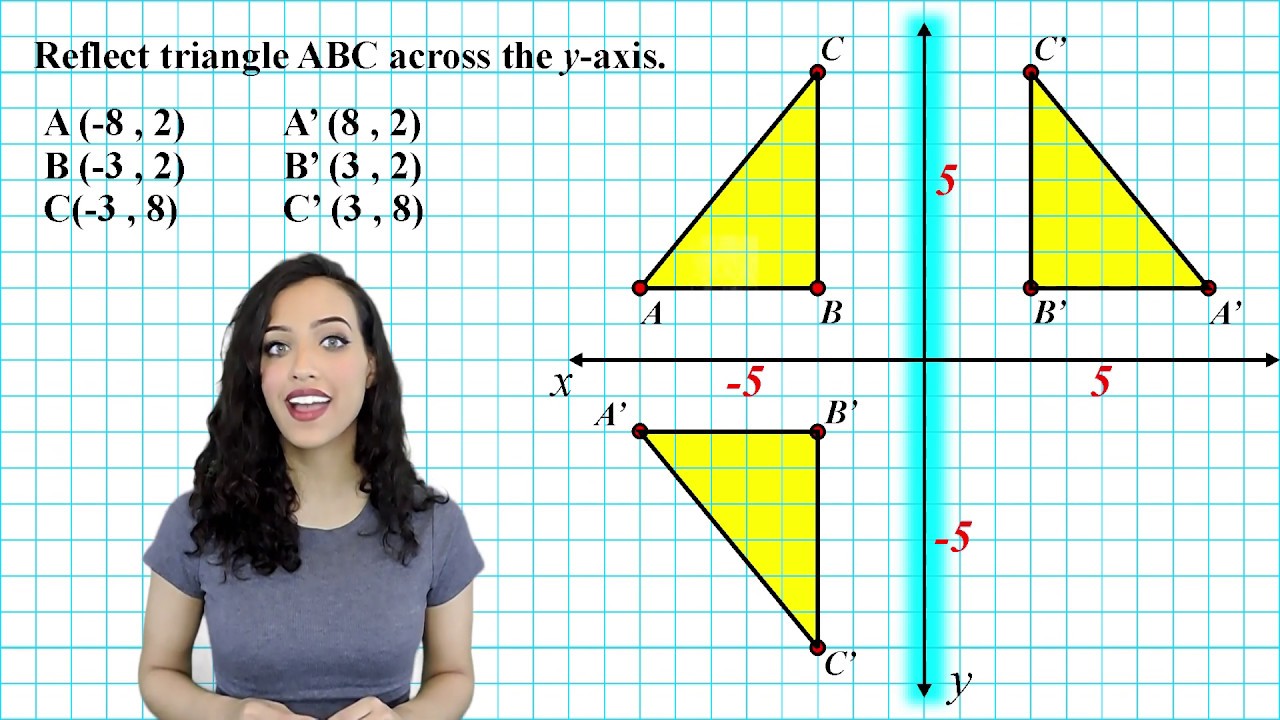
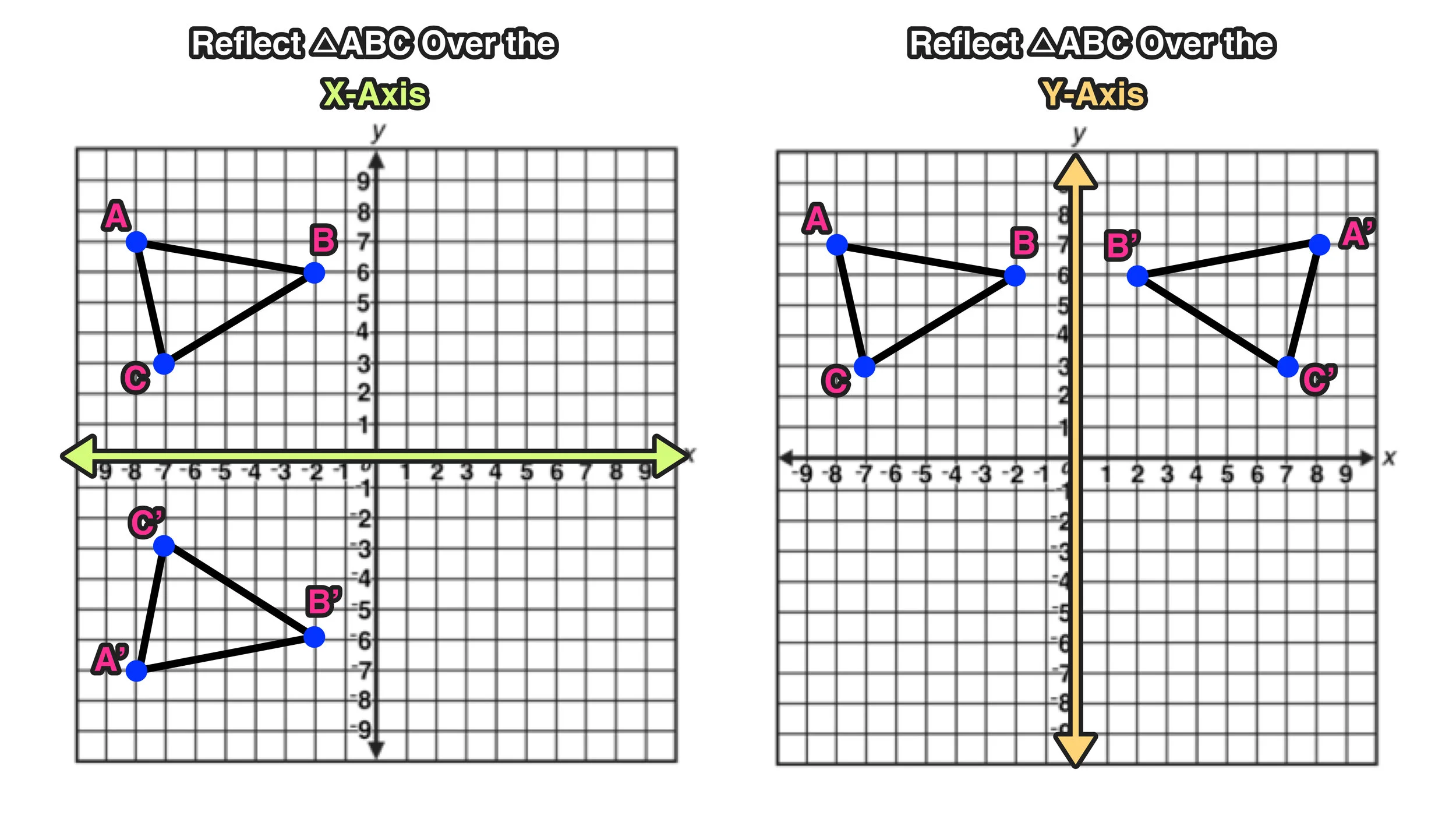
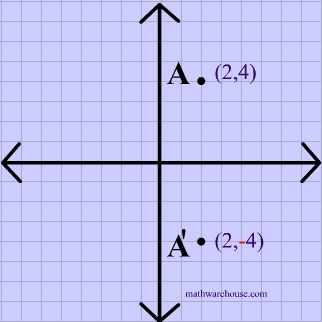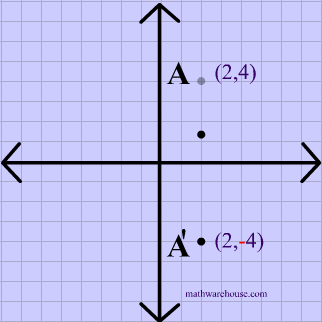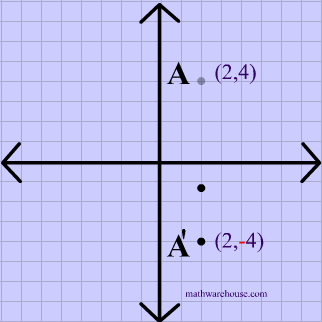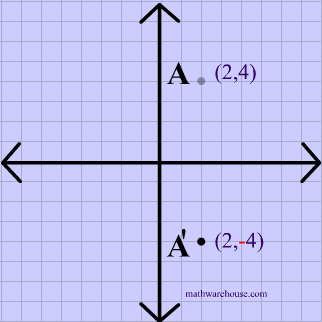
The reflection of the point ( x,y) across the xaxis is the point ( x,y ) Reflect over the yaxis When you reflect a point across the y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite (its sign is changed)A reflection can be done through yaxis by folding or flipping an object over the y axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directionsCorresponding parts of the figures are the same distance from the line of reflection Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y = x (y, x) This video shows reflection over the xaxis, yaxis, x = 2, y = −2 Show Video Lesson This video shows reflection over y = x, y = − x A reflection that results in



Reflection Rules Geogebra




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Reveal answer Remember \ (y = f (x) a \rightarrow\) translate up/down by the vector \ (\begin {pmatrix} 0 \\ a \end {pmatrix}\) \ (y = f (x a) \rightarrow\) translate left/right by the vectorWrite the Rules In these printable 8th grade worksheets write a rule to describe each reflection by determining if the reflection across the xaxis, across the yaxis or across a specific line Writing Coordinates With Graph Graph the image of each figure after the given reflection Label the image and write the coordinatesQuiz & Worksheet Goals In these assessments, you'll be tested on The rules that govern reflections across both the x and y axes individually Identifying y=x




Reflection Rules How To W 25 Step By Step Examples




Transformation Reflection Over The Line Y X Youtube
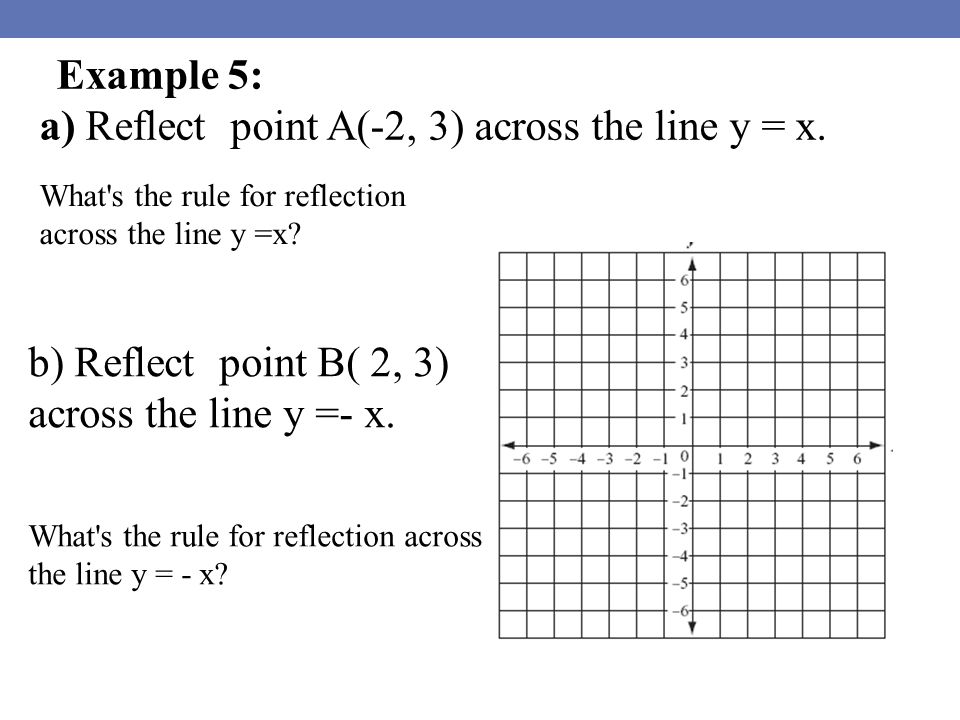
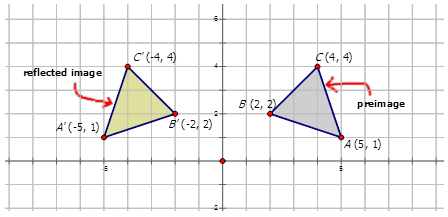
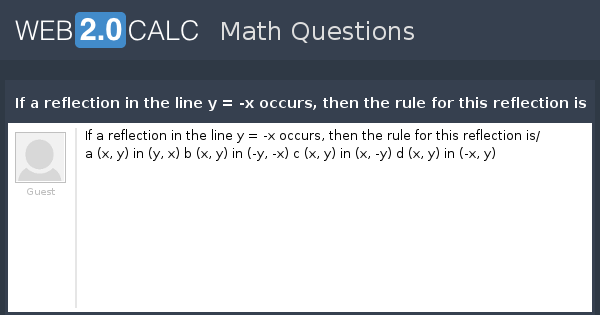
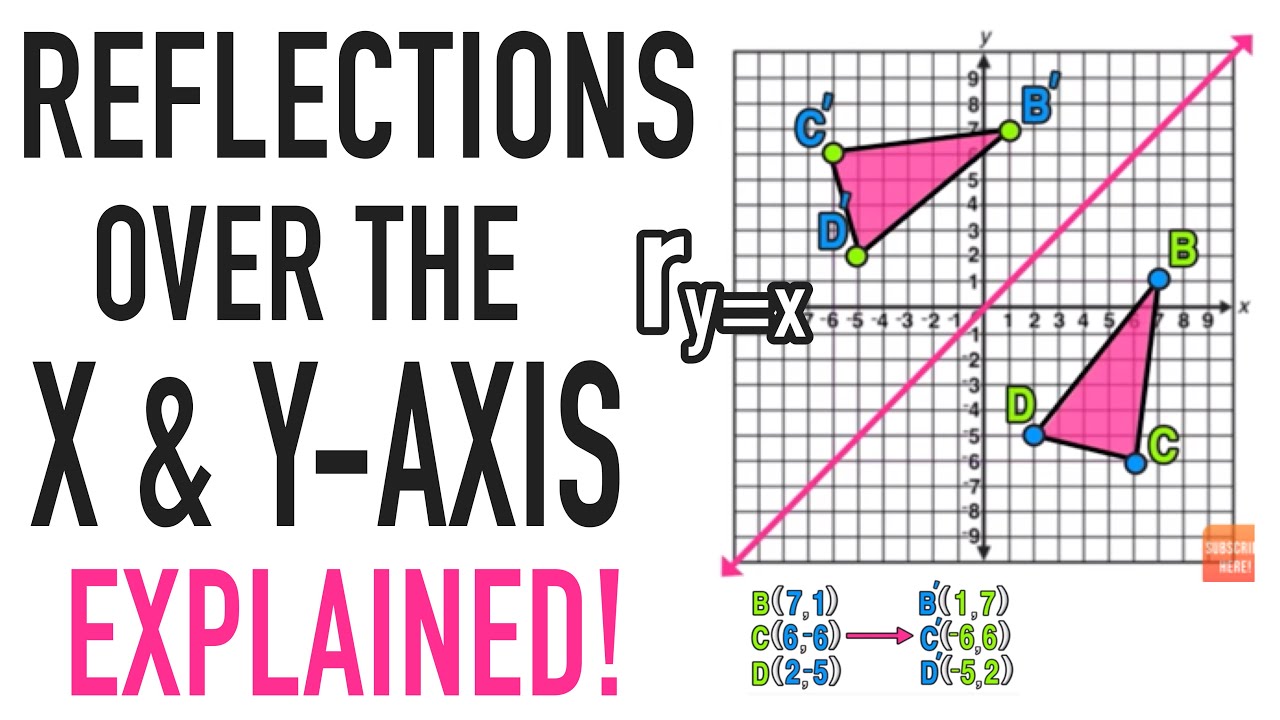
We have to identify the rules of reflection Firstly, the rule for reflecting a point about the line y=x is While reflecting about the line y=x, we get the reflected points by swapping the coordinates So, Option 3 is correct Now, the rule for reflecting a point about the line y= x isTriangle DEF is formed by reflecting ABC across the yaxis and has vertices D (4, 6), E (6, 2) and F (2, 4) All of the points on triangle ABC undergo the same change to form DEF Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x)Problem 1 Find a linear transformation rule of the form (p, q) → (r, s) such that the reflection image of the point (p, q) over the oblique line y = mx b is the point (r, s) In the general case, both r and s are functions of p, q, m and b



Solved Select The Best Answer For The Question 15 Find The Chegg Com



2
Shortcut rule for reflection of point over y axis The following steps will help you find the location of reflected image from y axis To locate the position of reflected point, follow the below steps;Reflection over the line y = x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x ( A, B) → ( B, A) Applet You can drag the point anywhere you want Reflection over the line y = − xReflections take two based on feedback from your in class assessments




Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Brainly Com




Rules For Reflections Read Geometry Ck 12 Foundation
In this video, you will learn how to do a reflection over a horizontal or vertical line, such as a reflection over the line x=1 Let's use triangle ABC with points A (6,1), B (5,5), and C (5,2) Apply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvaluesThe yvalue of P' is 10 The figure is an isosceles trapezoid How many lines of reflectional symmetry does the trapezoidWhich figure represents the image of parallelogram LMNP after a reflection across the line y = x?




Geometric Reflections Q35 50 Intro To Geometry




Quiz Worksheet Graphing The Origin Y X Reflections Across Axes Study Com
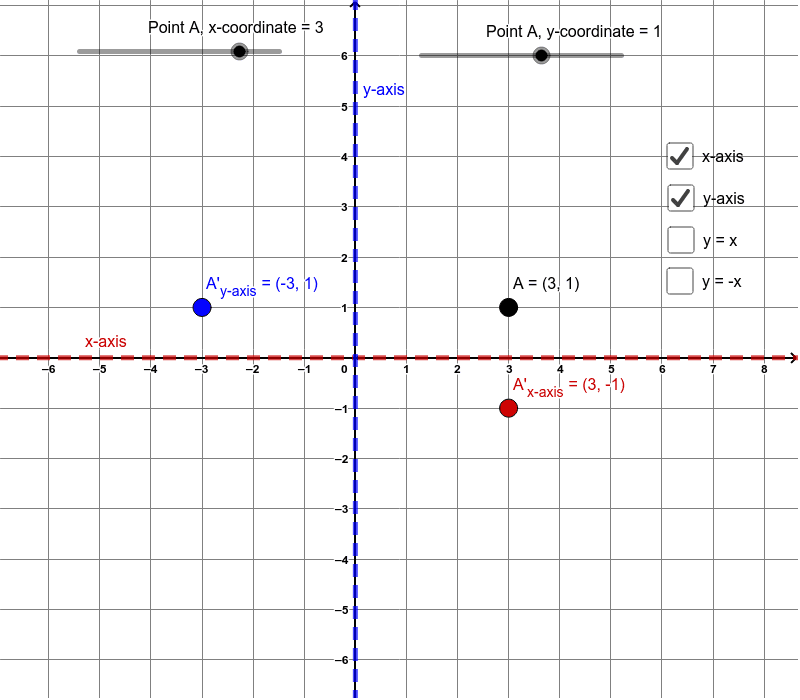
A reflection across the yaxis a reflection across the line y = x Stepbystep explanation In the image attached you can oberve that the order of tranformations is The first transformation is a reflection across the yaxis, notice that this axis works as a mirror, that indicates such reflection Also, when this reflection is applied, all xIf you reflect a point across the line y = x, the xcoordinate, and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places The line y = x is the point (y, x) the line y = x is the point (y, x)Therefore Image A has reflected across the xaxis To write a rule for this reflection you would write rx−axis(x,y)→(x,−y) Vocabulary Notation Rule A notation rule has the following form ry−axisA →B = ry−axis(x,y) →(−x,y) and tells you that the image A has been reflected across the yaxis and the xcoordinates have been




Reflections



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
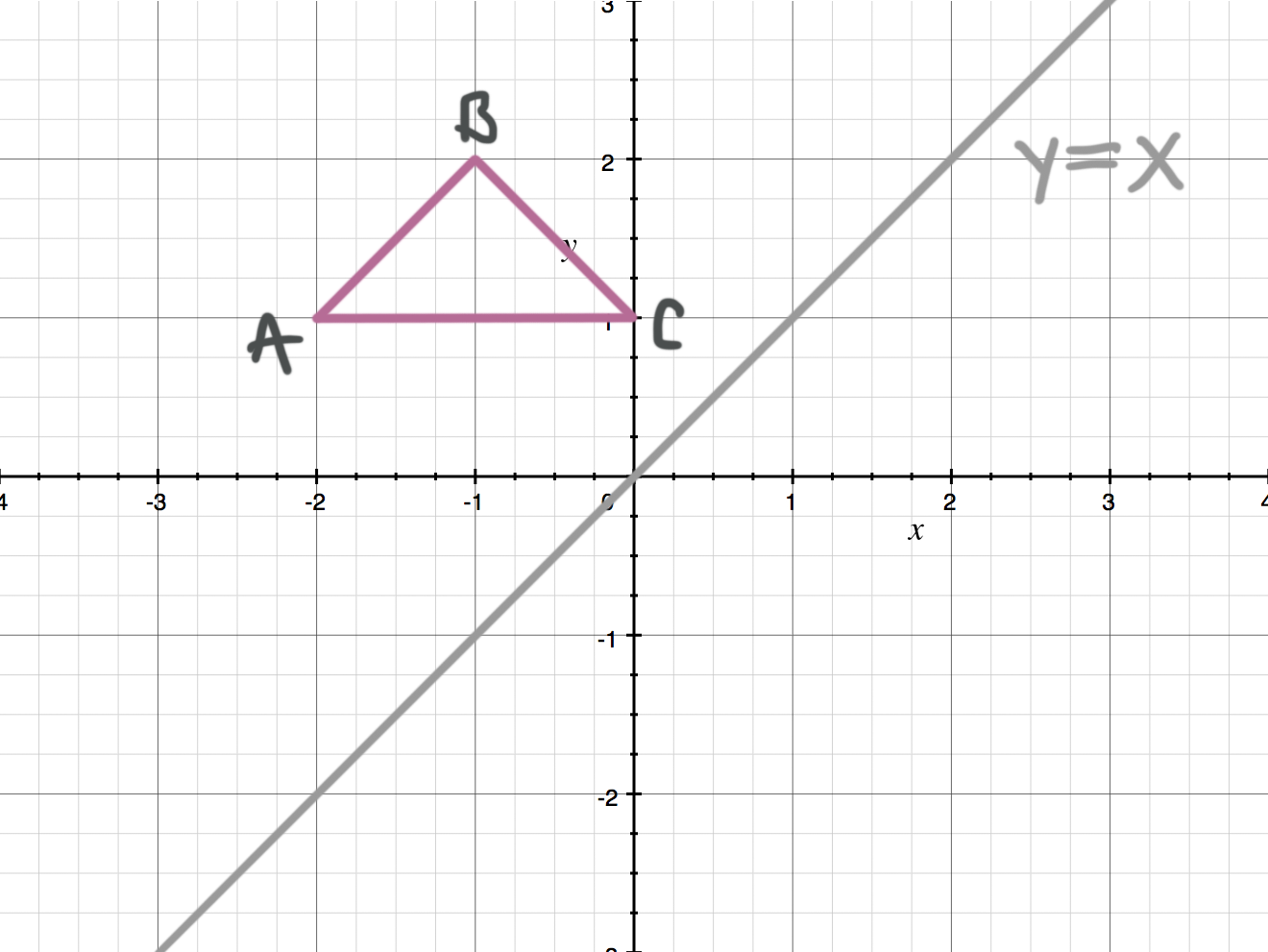
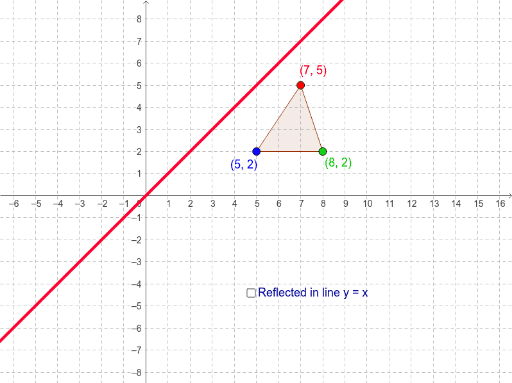
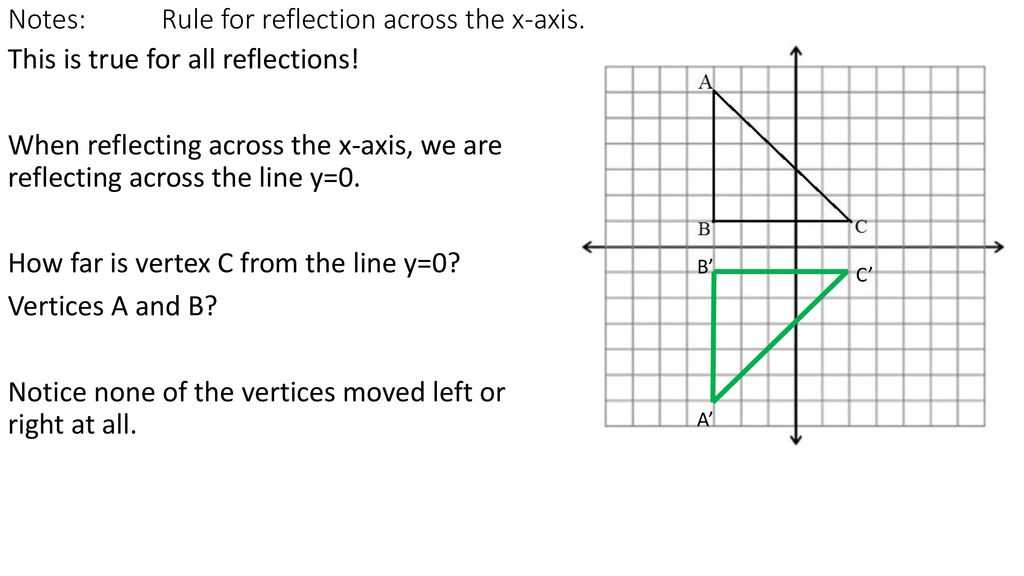
(x,−y) YAxis When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the Paper And when all else fails, just fold the sheet of paper along the mirror line and then hold it up to the light !Make sure the figure/line makes sense of where it isWhat is the rule for the following reflection?



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Rules How To W 25 Step By Step Examples
When you reflect this point, you should end up at the same "height" ( y coordinate) of − 5, but this time four units to the left of your axis of symmetry Four units to the left of x = − 1 is x = − 1 − 4 = − 5, so the point ( 3, − 5) reflects to ( − 5, − 5) We might write ( 3, − 5) → ( − 5, − 5) Similar reasoning shows that, for example,Change the sign of x coordinate of original point retain the same y coordinate Let us understand the above steps with following examples;If the preimage was reflected over the yaxis instead of the xaxis, what would the reflection rule be?




A Translation X Y X 5 Y Reflection Across Y Axis B Translation X Y X Y 5 Brainly Com



Reflection Across The X And Y Axis Youtube
Write a rule to describe each transformation 7) x y J V F K V' F' K' J' 11) x y A P U H P' U' H' A' reflection across the yaxis 12) x y Z D H U D' H' U' Z' reflection across y = x2Create your own worksheets like this one with Infinite Geometry Free trial available at KutaSoftwarecom Title 12Reflections Author Mike Created Date 7A reflection is a flip over a line You can try reflecting some shapes about different mirror lines here How Do I Do It Myself?Reflect the shape below in the line y = −x StepbyStep 1 Find the Cartesian coordinates of each point on the shape Write the xcoordinates and ycoordinates of each point 2 Change the sign of both coordinates Make them negative if they are positive and positive if they are negative 3
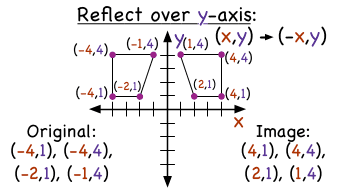



How Do You Use Coordinates To Reflect A Figure Over The Y Axis Virtual Nerd




Learn About Reflection Over The Line Y X Caddell Prep Online
Given points #A(1,2) , B (4,1)# Reflected across #x = 1#, #y = 3# #color(blue)("Reflection Rules "# #color(blue)("reflect over xaxis (x,y)"# #color(blue Reflection Over y = 2 With Rule by Lance Powell on image/svgxml Share The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Reflection In The Line Y X Geogebra
2 List the coordinates of the image if the preimage is reflected over the yaxis 3 If the preimage was located completely in Quadrant I, then reflected once over the xaxis and once over the yaxis, where would the image be?Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3) Reflection in y = x When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places What is a rule that describes the reflection?
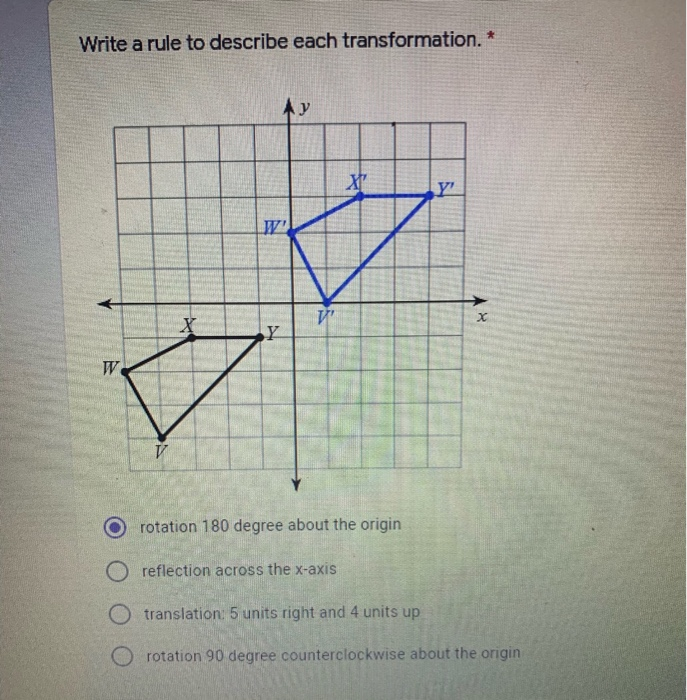



Solved Write A Rule To Describe Each Transformation Y Xt Chegg Com
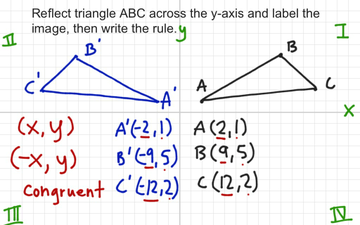



Reflection Across The Y Axis With Rule Educreations
I never learned a rule for reflection, but the easiest method would be to count the number of points the point of your figure/line from the x axis or yaxis, and apply the same number onto the other side That's how I always did it It you were to just move the whole figure over, that would only be translation! Reflection Across The Y Axis Rule To reflect a shape over an axis, you deserve to either enhance the distance of a point to the axis ~ above the other side of utilizing the reflection notation To complement the distance, you have the right to count the number of units come the axis and plot a suggest on the corresponding suggest over the axis Since the reflection applied is going to be over the xaxis, that means negating the yvalue As a result, points of the image are going to beA" (1,2), B" (3,5), and C" (7,1) By counting the units, we know that point A is located two units above the xaxis Count two units below the xaxis and there is point A'




Lesson 10 5 Transformations 1 Lesson 10 5 Transformations Ppt Download
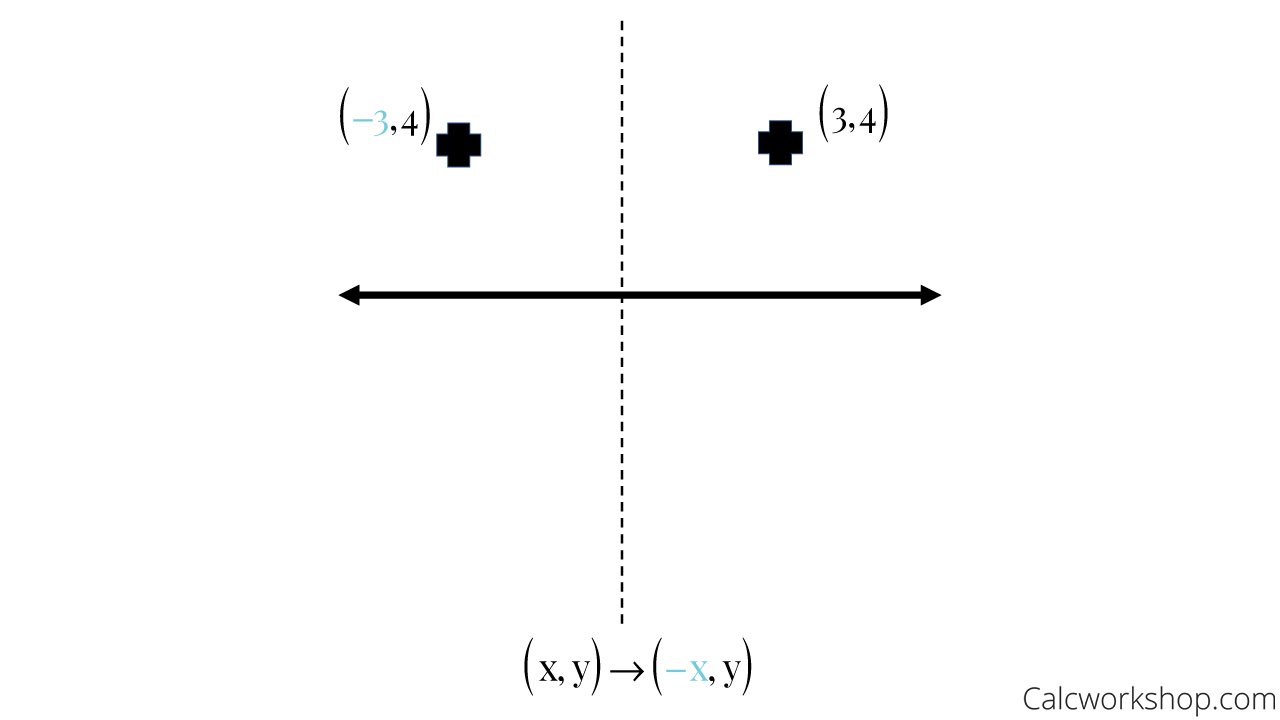



Reflection Rules How To W 25 Step By Step Examples
Answer choices Reflection across yaxis Reflection across xaxis Reflection across y = x Reflection across y = −x s Question 6 SURVEY 1 seconds A 180 o rotation about the origin followed by a reflection over the line y=x




Reflection Mathbitsnotebook A1 Ccss Math




How To Find A Reflection Image




Determining Reflections Video Khan Academy
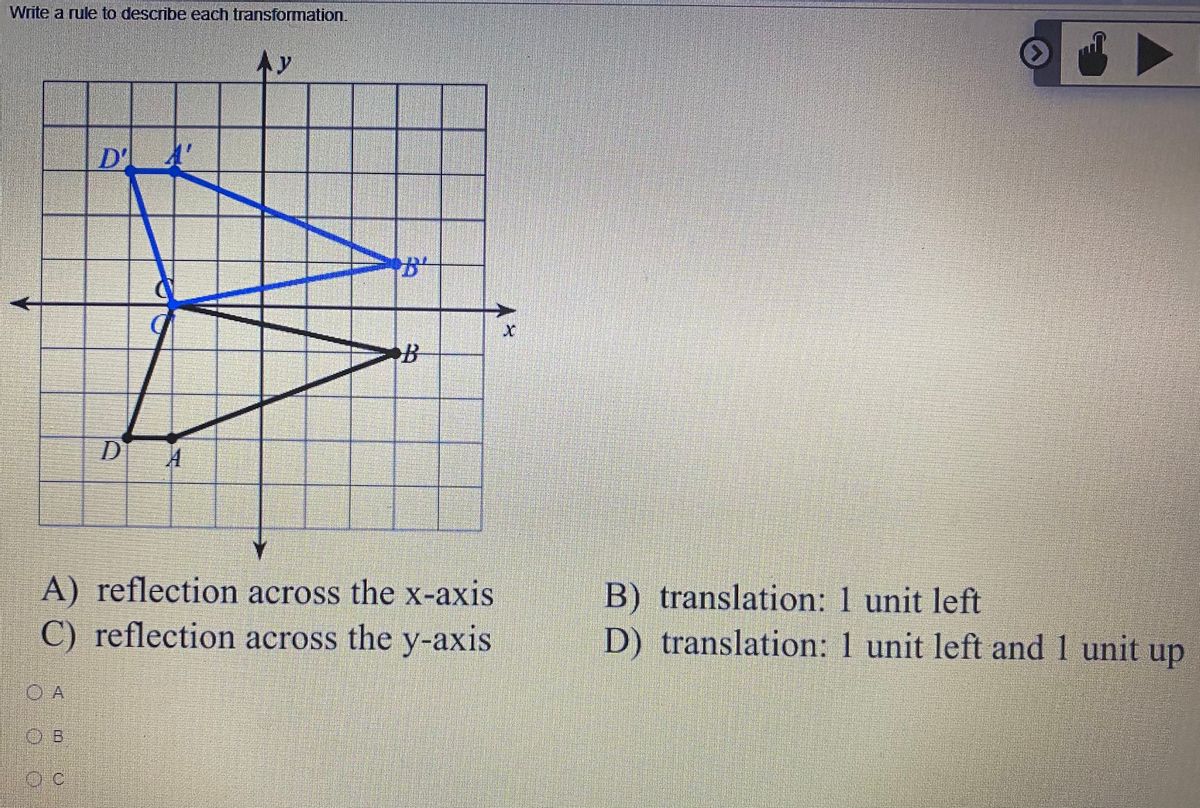



Answered Write A Rule To Describe Each Bartleby



Reflection Over Y X And Y X Youtube




Hw 6 Reflecting Over Y 1 Youtube




Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Transformation Matrix



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Rules For Reflections Read Geometry Ck 12 Foundation
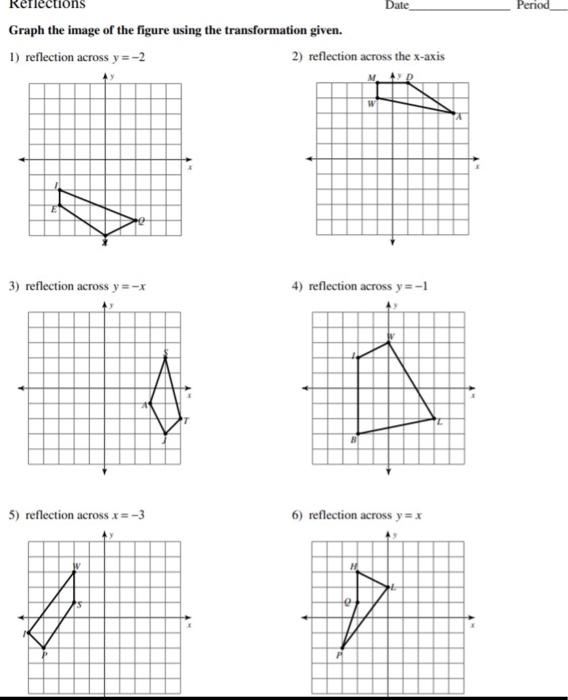



Solved Write A Rule To Describe Each Transformation 7 10 Chegg Com



What Is The Image Of 2 5 Reflected Across X 2 Socratic




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Rules How To W 25 Step By Step Examples




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Transformations Of Graphs
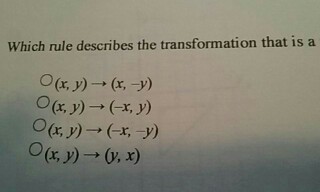



Solved Which Rule Describes The Transformation That Is A Chegg Com




Write A Rule To Describe Each Transformation What Is The Reflection Ex Reflect With Reaparece To Brainly Com




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
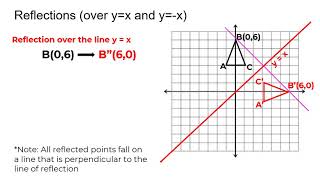



Reflection Over The Y X Line Youtube
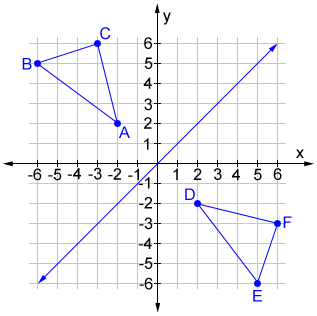



Reflection
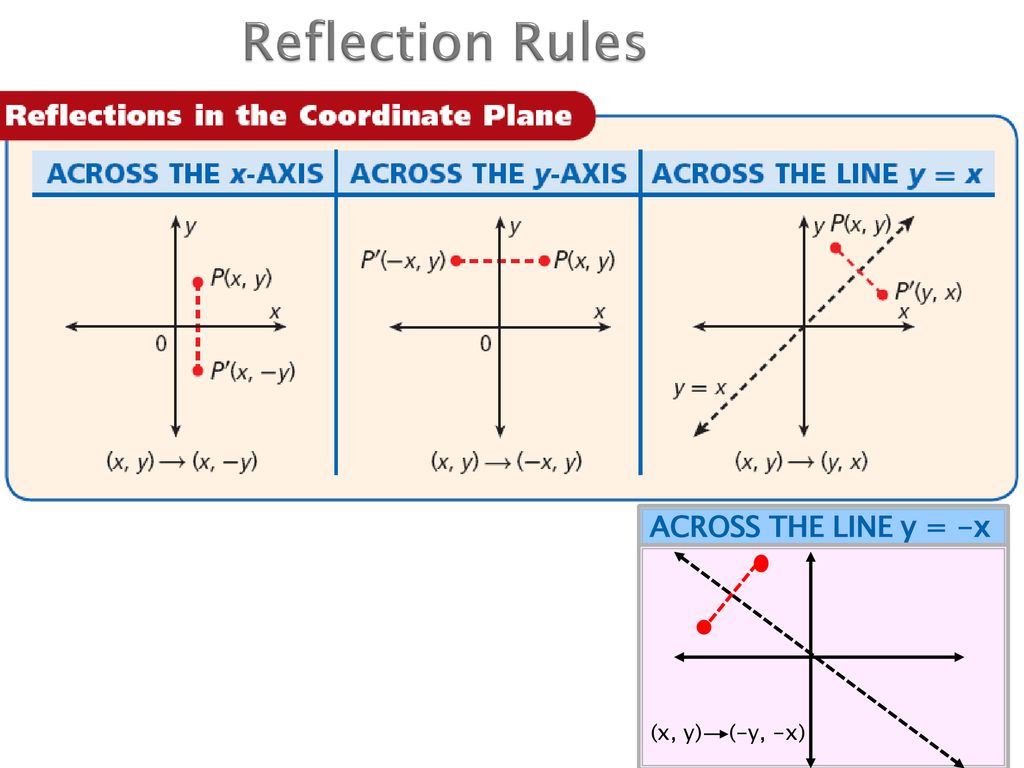



Pearson Unit 2 Topic 8 Transformational Geometry 8 2 Reflections Pearson Texas Geometry C 16 Holt Geometry Texas C Ppt Download



Common Core Math Geometric Reflection Over Y 2 Youtube
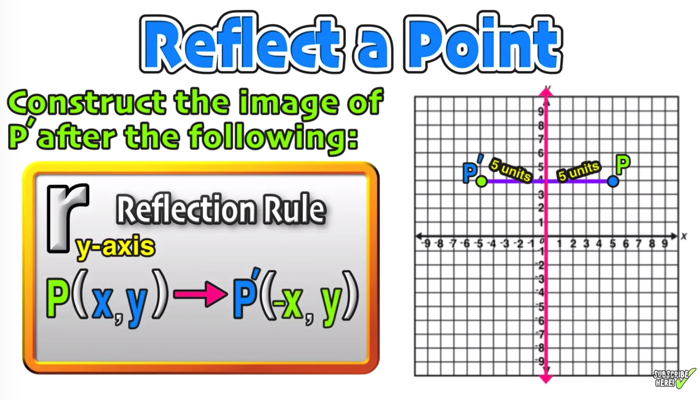



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflections Over The X Axis And Y Axis Explained Youtube



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Name Date Period Transformations Easter Break Packet



Rules For Reflections Read Geometry Ck 12 Foundation




Reflection Rules X Axis Y Axis Y X Y X Youtube



G67 Mini 6 6a Reflect An Image Across Y 1 Worksheet Tutorial Youtube




Solved Write A Rule In Function Notation To Describe The Chegg Com




How To Find A Reflection Image
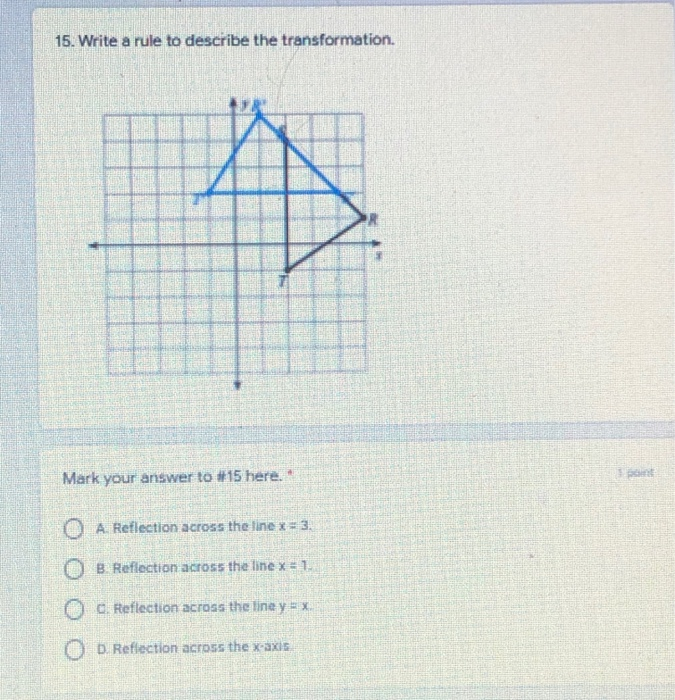



Solved S C 14 Find The Coordinates Of The Vertices Of The Chegg Com
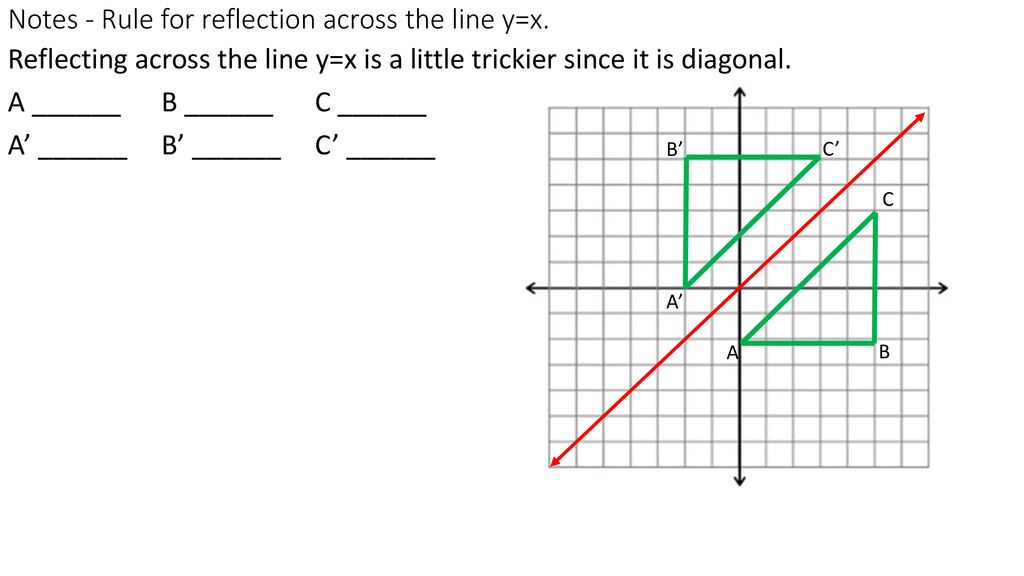



Unit 6 Day Ppt Download




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
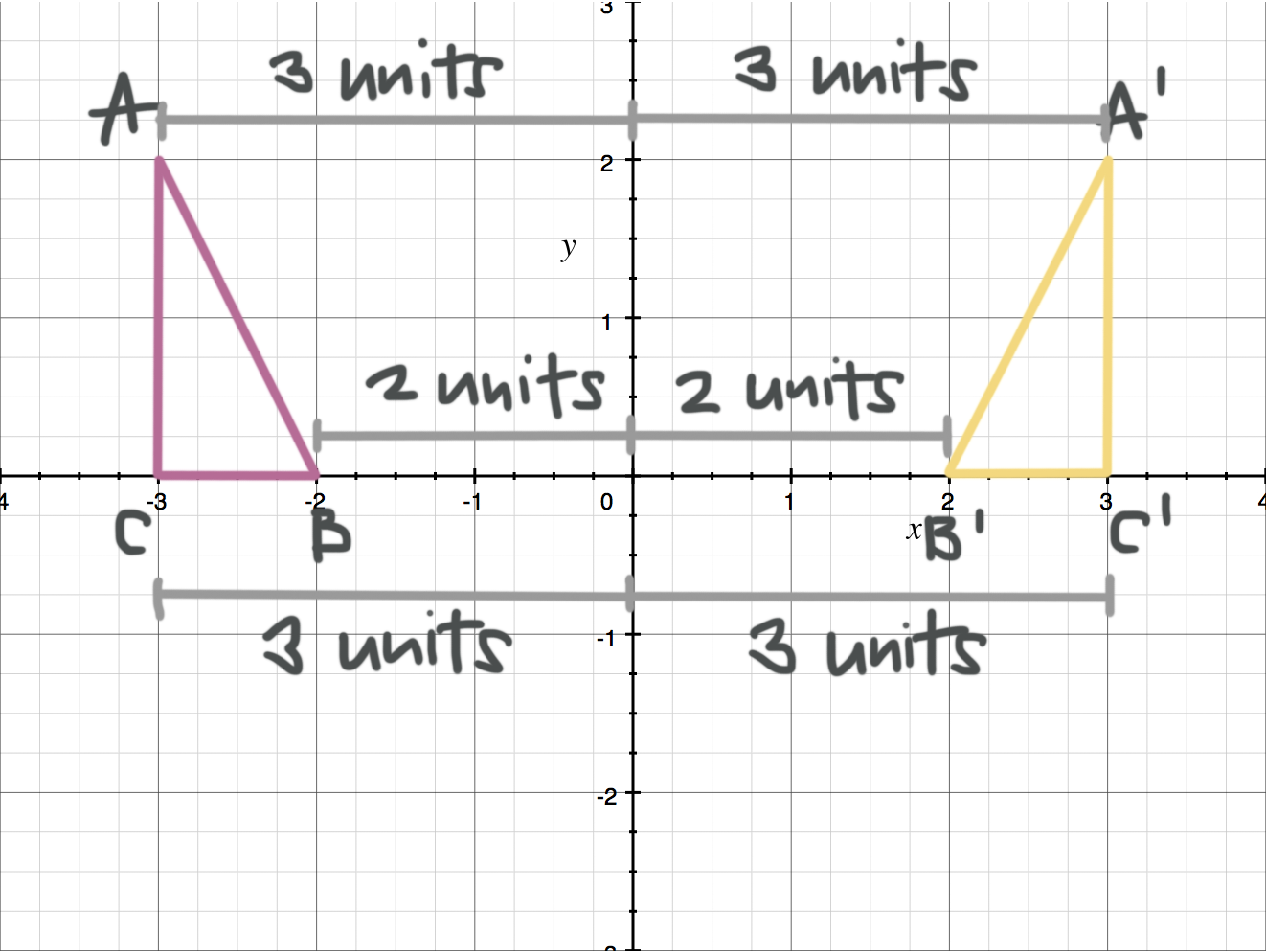



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




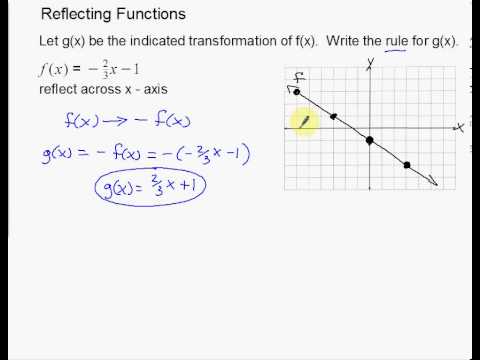
Reflecting Functions Examples Video Khan Academy



2
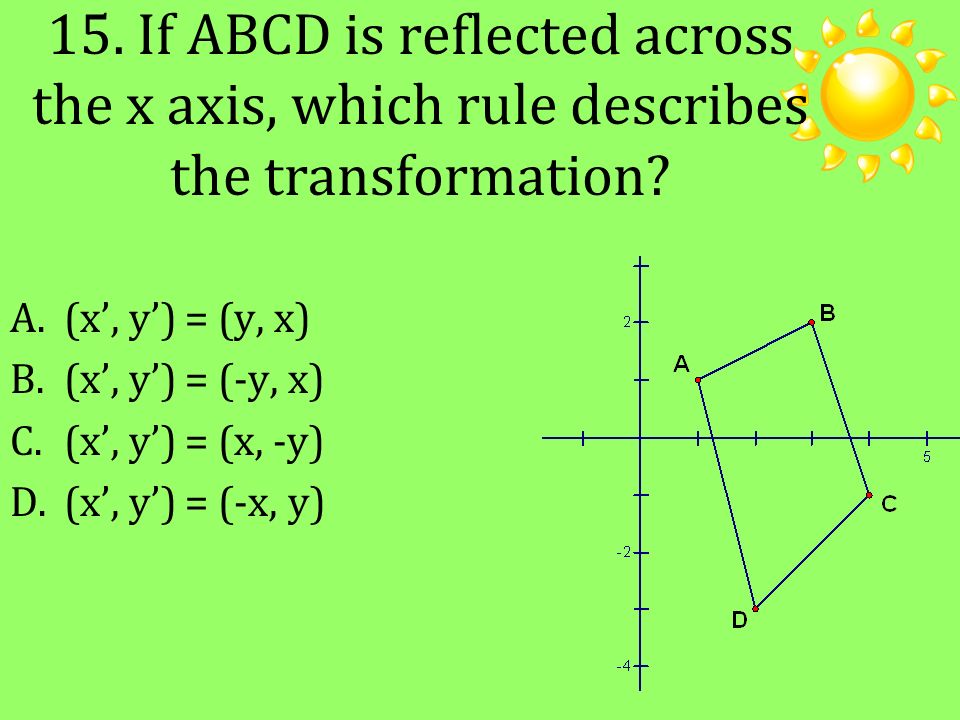



Warm Up Describe In Words How To Rotate A Figure 90 Degrees Clockwise Ppt Download



Unit 6 Day Ppt Download



Reflection Rules Toolkit



2




Reflection Rules How To W 25 Step By Step Examples




Reflection Over Y X Math Geometry Showme




Reflection Transformation Matrix




Reflection Over Y 2 With Rule Educreations




Reflection Transformation Matrix




9 2 Reflections Key Concepts R Stands For Reflection And The Subscript Tells You What To Reflect On Ex R X Axis The Line Of Reflection Is What Ppt Download



1




Reflection Transformation Matrix




Reflection Mathbitsnotebook A1 Ccss Math



View Question If A Reflection In The Line Y X Occurs Then The Rule For This Reflection Is



Reflection Rules How To W 25 Step By Step Examples




Reflections Ck 12 Foundation



1




D Reflection Across Y X Brainly Com



1



Reflection Across The Diagonal With Rule Educreations




Reflection Mathbitsnotebook A1 Ccss Math




60 Intro To Dilations 5 James Parson Library Formative




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities



Reflection Rules How To W 25 Step By Step Examples



Reflections Over The X Axis And Y Axis Explained Youtube




Reflection Over The X And Y Axis The Complete Guide Mashup Math



Linear Reflections Across X And Y Axis Example Youtube




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor




Kite Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection Brainly Com



Answered Rules For Reflections On A Coordinate Bartleby



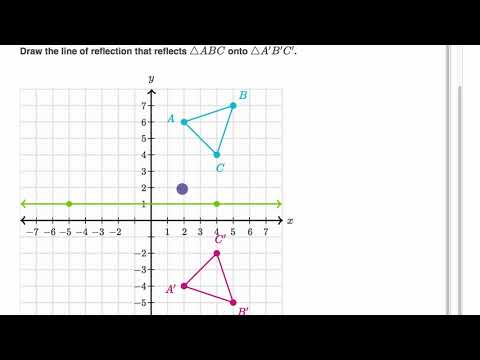
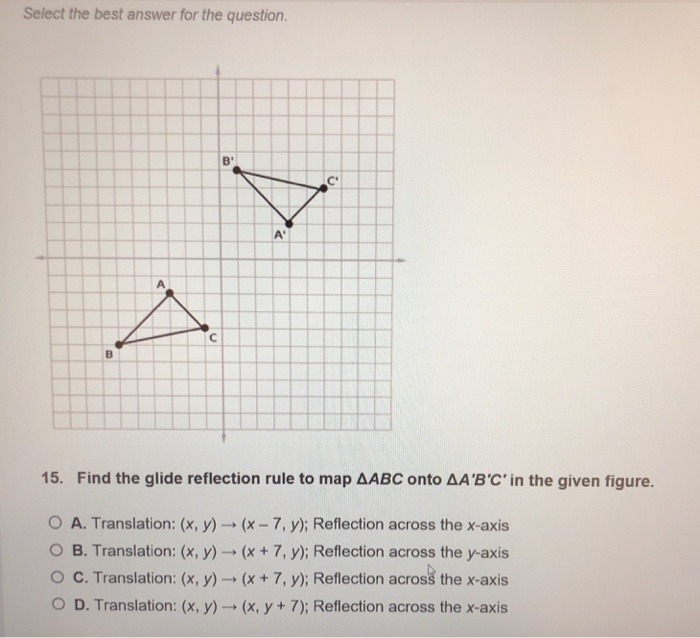
Solved Identify The Glide Reflection Rule To Map Abc Onto Abc In The Given Figure A Translation X Y X Y 4 Reflection Across The Y Course Hero



0 件のコメント:
コメントを投稿