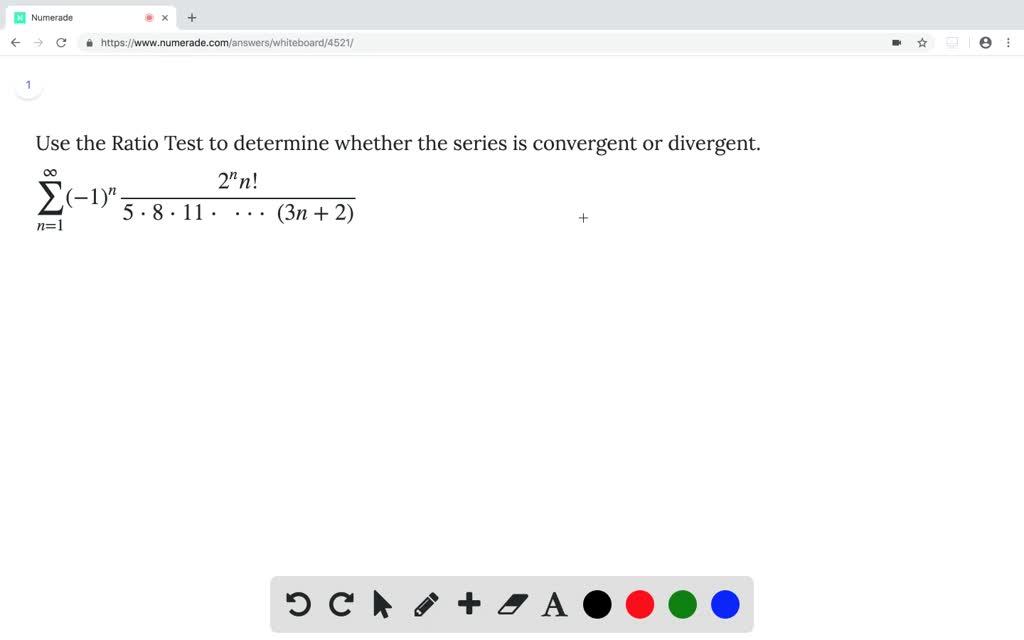
L = lim n → ∞ ( n 1) n!
2^n/n factorial convergence- A power series about a, or just power series, is any series that can be written in the form, ∞ ∑ n=0cn(x −a)n ∑ n = 0 ∞ c n ( x − a) n where a a and cn c n are numbers The cn c n 's are often called the coefficients of the series The first thing to notice about a power series is that it is a function of x xAnswer (1 of 4) Let A_n = \frac{(n!)^2}{(2n)!} Apply the ratio test, also known as the Cauchy ratio or D'Alembert ratio test We calculate \begin{align*}\lim_{n\to
2^n/n factorial convergenceのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  |  |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 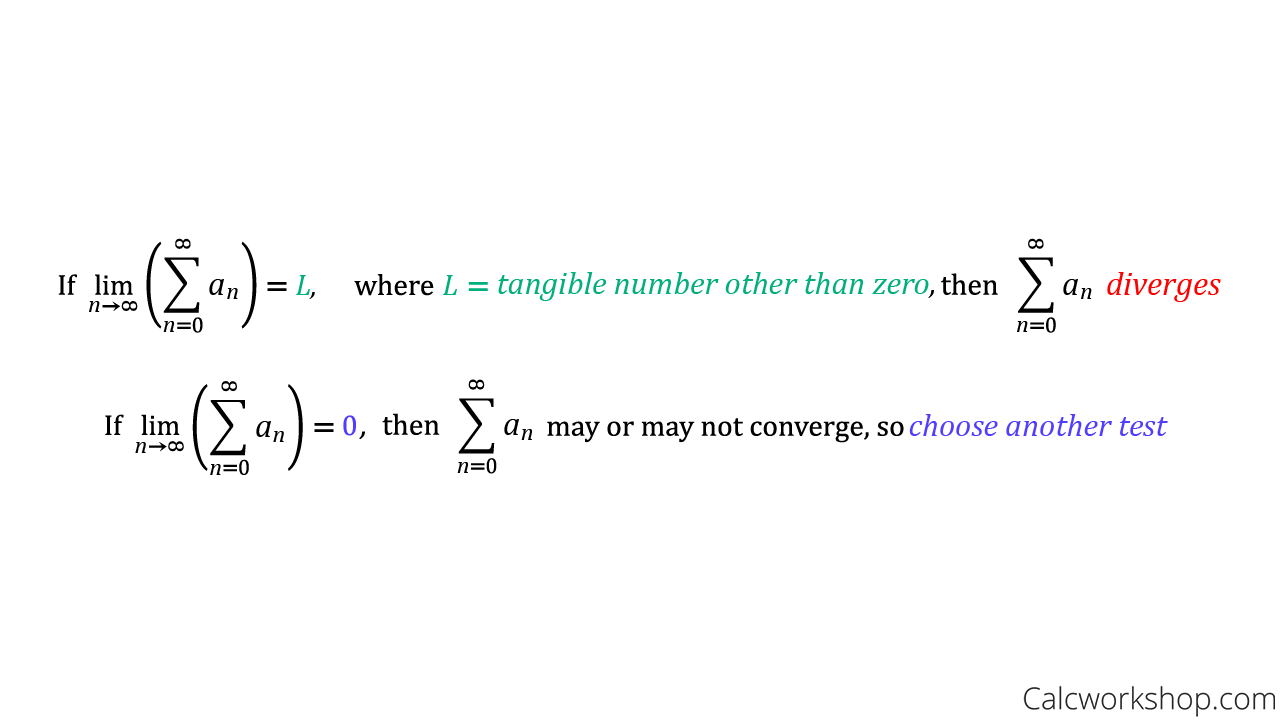 |  |
 |  |  |
 |  | |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 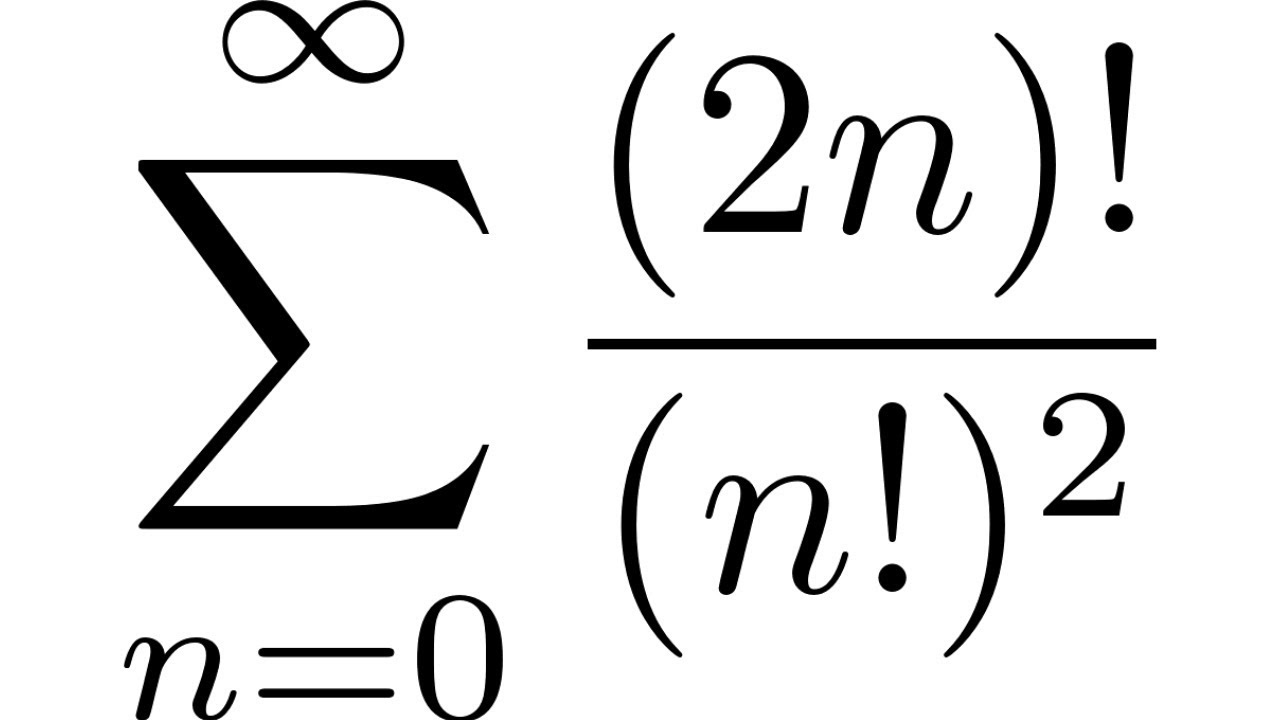 |
 |  |  |
 |  |  |
 | ||
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「2^n/n factorial convergence」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |
The facthttps//wwwyoutubecom/watch?v=HMkwHR4VO4&t=5s , the fact again, https//wwwyoutubecom/watch?v=2nUJMP_ZnnI&t=27s , series of n^n/(n!)^2, limit oSo bn/bn1=1 now lim n>infinity bn (bn/bn11)=lim n>infinity n/n1 ×0=1×0=0





0 件のコメント:
コメントを投稿